Конспект уроку: Побудова зображень, що дає тонка лінза. Формула тонкої лінзи

Умовне зображення лінзи

Для спрощення малюнків при побудові зображень предметів в тонких лінзах домовимося зображати їхніх відрізками, що лежать в площині лінзи.

Ви бачите умовні зображення збиральної й розсіювальної лінз.

Як приклад, покажемо знаходження зображень точок в збиральній й розсіювальній лінзах із використанням їхніх умовних зображень.

Предмети здатні бути на різноманітних відстанях від лінзи, саме тому при побудові їхніх зображень додатково виділимо на головній оптичній осі ще дві точки, розміщені на подвійній фокусній відстані від неї. Можливі подібні випадки:

- відстань до предмети більша подвійної фокусної відстані, тобто d › 2F

- предмет перебуває на подвійній фокусній відстані d = 2F

- предмет перебуває між фокусом й подвійною фокусною відстанню F ‹ d ‹ 2F

- предмет на фокусній відстані d = F

- предмет між фокусом й лінзою d ‹ F

Розглянемо будь-який із них окремо.

d › 2 F

Умовно зобразимо предмет стрілкою, нижній край котрої лежить на головній оптичній осі. Зображення точки А теж буде на головній оптичній осі.

Побудуємо зображення точки У.

Зображення предмета являється дійсним, зменшеним у порівнянні із розміром предмета, оберненим та розташований між фокусом та подвійним фокусом лінзи.

Таким чином, якщо відстань до предмети більша подвійної фокусної відстані (d › 2F), то зображення формується між фокусом та подвійною фокусною відстанню (F ‹ f ‹ 2F) .

d = 2 F

Наблизимо предмет до лінзи та помістимо його на відстані, що дорівнює подвійній фокусній.

Зображення буде на подвійній фокусній відстані, обернене; дійсне та за розміром рівне предмету.

Якщо предмет наближається до лінзи, його зображення віддаляється та за розміром збільшується.

Тобто, якщо d = 2F, то f = 2F

F ‹ d ‹ 2 F

Наблизимо предмет до лінзи, аби він являвся між її фокусом й подвійною фокусною відстанню. Зображення залишилось оберненим, віддалилося, стало більшим за розмір предмета, й залишилося дійсним.

Якщо F ‹ d ‹ 2F , то f › 2F

d = F

Якщо предмет поставити так, аби точка А знаходилась в фокусі лінзи, всі промені, що виходять із неї, після заломлення у лінзі, підуть паралельно головній оптичній осі, тобто зображення її не буде (промені не перетинаються). Саме тому ми не одержимо зображення предмета.

Якщо d = F, зображення немає.

d ‹ F

При переміщенні предмета на відстань, меншу фокусної відстані F наперед можна сказати, що, ми не одержимо зображення справа, адже, при d = F, зображення уже не існує.

Наші міркування підтверджує малюнок, котрий показує хід променів від предмета, за умови

d ‹ F.

Якщо відстань предмета від лінзи менша фокусної, його зображення буде збільшеним, уявним, прямим (не перевернутим) та розташований по той же сторона від лінзи, що та предмет.

Висновки

1. З допомогою лінзи можна отримати збільшене чи зменшене зображення предмета, у залежності від його положення відносно лінзи.

2. Зображення здатний бути дійсним, тобто промені, реально перетинаючись, створюють його, чи уявним, тобто реально не існуючим, однак нам здається, що промені, котрі пройшли через лінзу, виходять із точок, що й створюють уявне зображення.

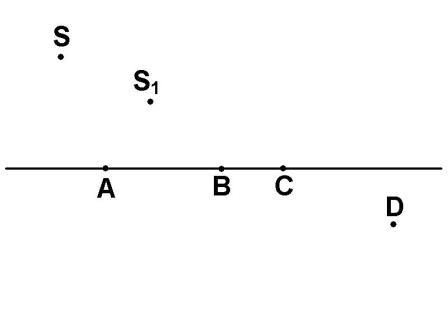
3. Лінзі притаманна оборотність променів. Це значить, що якщо світна точка S має власне дійсне зображення у точці S', то, помістивши світну точку у S', ми одержимо її дійсне зображення у точці S.

Аналогічною буде картина із будь-яким предметом й його зображенням.

Побудова зображень у розсіювальній лінзі

Зображення предмета АВ у розсіювальній лінзі являється уявним, зменшеним, прямим та розташований між фокусом лінзи і її оптичним центром.