Конспект уроку: Змочування. Капілярні явища. Явища змочування і капілярності в живій природі і техніці

Змочування

Важливу роль у процесі дослідження контактної взаємодії рідини із твердим тілом відіграє явище змочування.

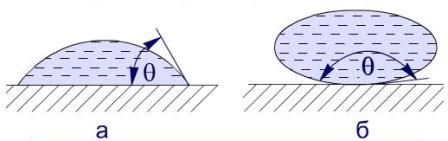
Рис. Змочування і незмочування рідиною поверхні твердого тіла. Коли нанести краплю рідини на поверхню твердого тіла, то вона за певних умов набуде граничних конфігурацій, представлених на рисунку (а, б).

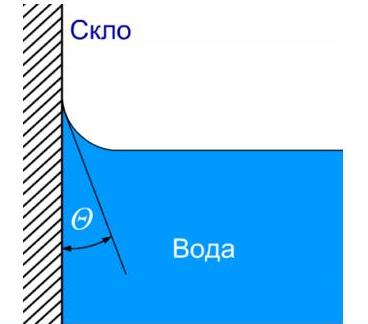
Рис. Вільна поверхня рідини біля стінок посудини при змочуванні

Аналогічно до форми краплі рідини на поверхні твердого тіла, вільна поверхня рідини біля стінок посудини є викривленою. Отже явище змочування полягає в викривленні вільної поверхні рідини на границі дотику з твердим тілом. Викривлена поверхня рідини називається у цьому випадку меніском. Явище змочування може характеризуватися крайовим кутом між поверхнею твердого тіла й меніском.

При змочуванніНаприклад, вода змочує скло, ртуть змочує цинк.

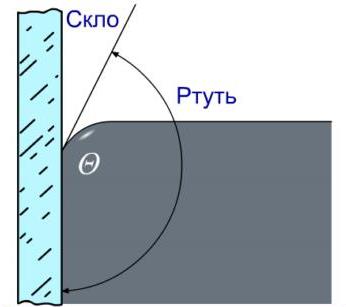
Рис. Вільна поверхня рідини біля стінок посудини

Візуально явище змочування можна спостерігати в викривленні вільної поверхні рідини на границі дотику з твердим тілом. Воно характеризується крайовим кутом між поверхнею твердого тіла й меніском.

При незмочуванніНаприклад, ртуть не змочує скло, вода не змочує парафін.

З’ясуємо умови, за яких мають місце явища змочування або незмочування. Для цього виконаємо прості досліди.

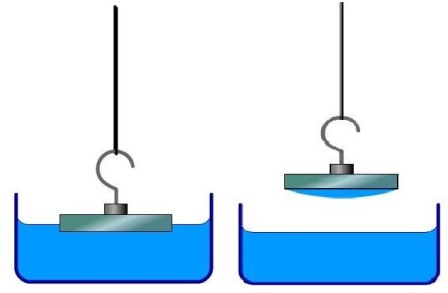
Рис. Спостереження явищ змочування

Етап 1.

Візьмемо скляну пластинку, на якій зверху закріплено гачок, і покладемо її на поверхню води.

Етап 2.

Будемо тягнути за гачок до моменту відриву пластинки від води. Бачимо, що відірвана скляна пластинка покрита водою. У цьому випадку розрив відбувся між молекулами води, а не між водою і склом. Це означає, що сили взаємодії між водою і склом перебільшують сили взаємодії поміж молекулами води.

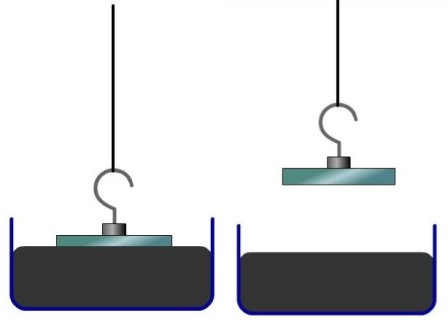
Рис. Спостереження явищ незмочування

Етап 1.

Візьмемо скляну пластинку, на якій зверху закріплено гачок, і покладемо її на поверхню ртуті.

Етап 2.

Відриваємо пластинку від поверхні ртуті і бачимо: ртуті на пластинці немає. Це свідчить про наступне - сили притягання між молекулами скла і ртуті менші за сили притягання поміж молекулами ртуті.

Отже, явища змочування й незмочування пояснюються співвідношенням між силами притягання молекул твердих тіл і рідин та силами міжмолекулярного притягання у рідинах. Коли ж сили притягання поміж молекулами твердого тіла й рідини перебільшують сили притягання між молекулами рідини, то тоді рідина змочує тверде тіло. Якщо міжмолекулярне притягання у рідині перевищує сили притягання молекул рідини до молекул твердого тіла, то тоді рідина незмочує тверде тіло.

Капілярні явища

У природі часто зустрічаються пористі тіла, об’єм яких пронизаний великою кількістю дрібних каналів. Таку будову мають папір, шкіра, дерево, грунт, деякі будівельні матеріали. Вода або інша рідина при попаданні на таке тіло убирається в нього або підіймається на значну висоту. Аналогічні явища можна спостерігати також у дуже вузьких скляних трубках з діаметром біля міліметра і менше, які називаються капілярами.

Явища, що зумовлені поверхневим натягом і відбуваються в тонких трубчатих каналах (капілярах), називаються капілярними явищами або капілярністю.

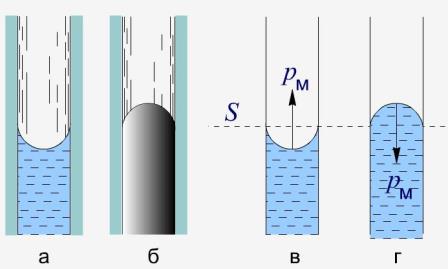
Рис. Форма менісків для змочуючої і незмочуючої рідин.
Якщо капіляр опустити у рідину, то вона буде підійматись по його стінках, при цьому вся вільна поверхня рідини у капілярі буде викривленою. У випадку змочуючої рідини викривлена поверхня рідини (тобто, меніск) буде спрямована вниз (а), а у випадку незмочуючої - вгору (б).

Викривлена поверхня рідини утворює додатковий тиск на рідину у порівнянні із тиском під плоскою поверхнею. За увігнутого меніску тиск під плоскою поверхнею S стає меншим на величину додаткового тиску ри. За опуклого меніску додатковий тиск рм збільшує тиск, котрий існує під плоскою поверхнею рідини, в тому числі, атмосферний тиск на вільну поверхню рідини.

Додатковий тиск для сферичної поверхні рідини вираховується за формулою:

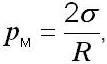
де Ϭ – це коефіцієнт поверхневого натягу, R – це радіус сферичної поверхні; рм < 0, коли меніск увігнутий; рм > 0, коли меніск опуклий.

Дана формула зветься формулою Лапласа, названа на честь відомого французького математика, астронома та фізика П’єра Симона Лапласа, котрий вперше отримав її.

Деякі закономірності цих капілярних явищ.

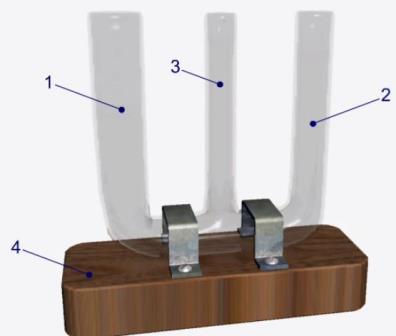
Рис. Залежність висоти стовпчика рідини в капілярі від його діаметра (для змочуючої рідини)

Етап 1.

Для досліду застосуємо спеціальний набір трубок, дві з яких (2, 3) є капілярними. Діаметр капіляру 2 дорівнює 2 мм, капіляру 3 - 1 мм, діаметр широкої трубки 1 - 6 мм. Висота трубок - близько 5 см. Трубки забезпечені підставкою 4 для зберігання.

Для заповнення трубок рідиною зручно користуватися піпеткою внаслідок малого діаметра капілярних трубок.

Етап 2.

Накапаємо з піпетки у широку трубку стільки забарвленої води, щоб її рівень у найтоншому капілярі не доходив до верху. Пунктиром вказано рівень рідини в трубці найбільшого діаметру.

Отже, коли має місце явище змочування, тоді рідина в капілярах встановлюється вище рівня рідини в широкій трубці, тоді як висота підняття рідини являється найбільшою у капілярі з меншим радіусом.

Якщо має місце явище змочування, то рідина у капілярах встановлюється вище від рівня рідини у широкій трубці, а висота підняття рідини є найбільшою в капілярі із меншим радіусом.

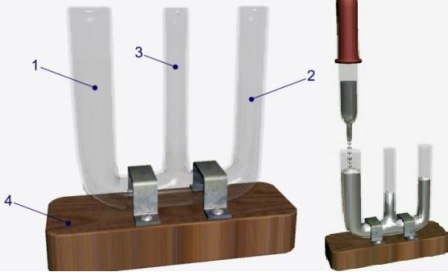
Рис. Залежність висоти стовпчика рідини в капілярі від його діаметра (для незмочуючої рідини)

Етап 1.

Виконаємо аналогічний дослід з рідиною, яка не змочує скло - ртуттю. Для цього використаємо той же набір трубок.

Етап 2.

За допомогою піпетки заповнимо капіляри ртуттю. Пунктиром вказано рівень рідини в трубці найбільшого діаметру.

Бачимо, що у випадку, коли має місце явище незмочування. рідина в капілярах установлюється нижче рівня рідини в широкій трубці, а зниження рівня рідини являється найбільшим в капілярі із меншим радіусом.

Коли має місце явище незмочування, рідина в капілярах установлюється нижче рівня рідини в широкій трубці, а зниження рівня рідини являється найбільшим в капілярі із меншим радіусом.

Для підйому рідини у капілярі має місце закон Жюрена:

висота підняття рідини у капілярі пропорційна коефіцієнту поверхневого натягу рідини й обернено пропорційна радіусу капіляра і густині рідини. Отже,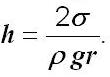

Формула Жюрена застосовується й до капілярної трубки зі незмочуючою рідиною, однак у даному випадку вираховується не висота підняття рідини, а вже зниження її рівня.

Формулу Жюрена також можна застосовувати для визначення коефіцієнту поверхневого натягу. Необхідно тільки точно виміряти висоту підняття h й радіус капіляра r. Тоді за відомими значеннями р й g із формули Жюрена отримується значення. Це один із найбільш поширених методів для визначення коефіцієнту поверхневого натягу будь-якої рідини.

Явища змочування й капілярності у живій природі і техніці

Явище змочування отримало велике практичне значення. Його використовують у процесах паяння, склеювання, змащення тертьових поверхонь, фарбування тіл і т.п. Особливо широко використовуються змочування в флотаційних процесах (збагачення руд цінною породою). У основу даних процесів покладена зміна поверхневого натягу рідини з допомогою різних домішок й неоднакове змочування нею різноманітних твердих тіл.

Сутність принципу флотації полягає у наступному. Чиста руда майже ніколи не зустрічається в природі. Корисна копалина здебільшого перемішана з непотрібною порожньою породою (бідна руда). Перш ніж використати у виробництві, її необхідно збагатити, тобто відокремити руду від породи. Флотаційний процес полягає у прилипанні бульбашок повітря до частинок корисної копалини. Густина корисної копалини і бульбашки повітря менша за густину води, тому вони спливають. Отже, флотація можлива за таких умов:

1) поверхня частинок корисної копалини не повинна змочуватись водою;

2) руда має бути роздрібнена на такі частинки, щоб вони могли спливати з бульбашками повітря, які до них прилипають. Для покращення процесу прилипання бульбашок повітря до частинок корисної копалини у флотаційну ванну додають олію, яка змочує частинки корисної копалини і не змочує частинки породи. Бульбашки повітря добре прилипають до покритих тонкою плівкою олії частинок корисної копалини.

При механічній обробці металів, бурінні свердловин в гірських породах змочують їх спеціальними рідинами, котрі полегшує й прискорює їх обробку.

Подібне явище змочування потрібно враховувати й в конструюванні космічних апаратів. У стані невагомості змочуюча рідина розпливається по бокових стінках посудини, а незмочуюча збирається в посудині у вигляді великої краплини. Тому матеріал стінок й форму ємностей для палива треба вибирати так, аби паливо втримувалось біля отворів, крізь які воно перекачується до двигунів.

Надзвичайно поширена у природі, техніці та побуті капілярність, яка відіграє значну роль у багатьох процесах.

Зокрема, у будівельній практиці необхідно враховувати піднімання вологи по капілярах будівельних матеріалів. Цегла та бетон мають широко розгалужені системи капілярів, по яких вода може підніматись на велику висоту, спричиняючи вологість стін будинку. З метою захисту стін від вологості між фундаментом будинку і стінами прокладають шар толю, смоли чи іншого матеріалу, котрий перешкоджає проникненню вологи.

Капілярні явища важливі й у житті рослин, людей і тварин (в тілі дорослої людини біля 160 мільярдів капілярів, загальна довжина котрих 60 - 80 тисяч км). Саме у капілярах здійснюються основні процеси, які пов’язані із диханням й живленням організмів.

На капілярних явищах ґрунтуються агротехнічні прийоми регулювання водного режиму ґрунту - закоткування і боронування.

Явище капілярності використовують й у побуті, наприклад при застосуванні гігроскопічної вати, промокального паперу, рушників та серветок.